三 平方 の 定理 の 利用 351602
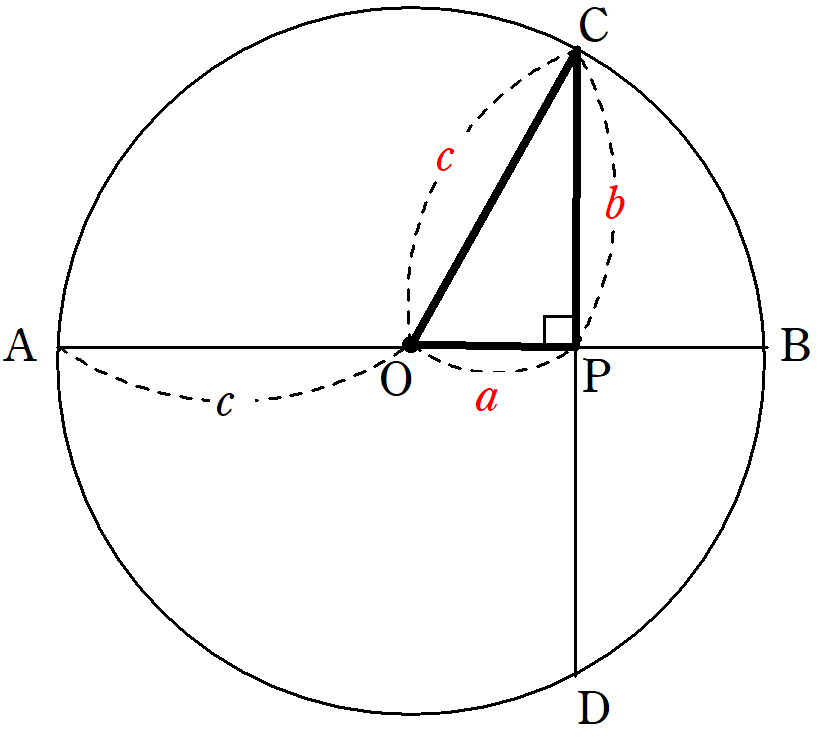
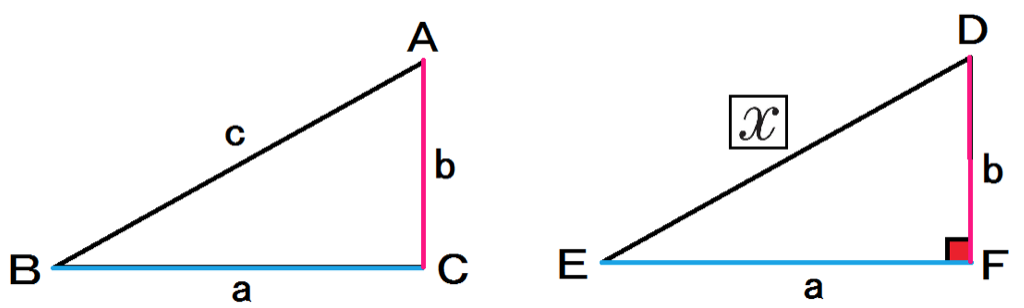
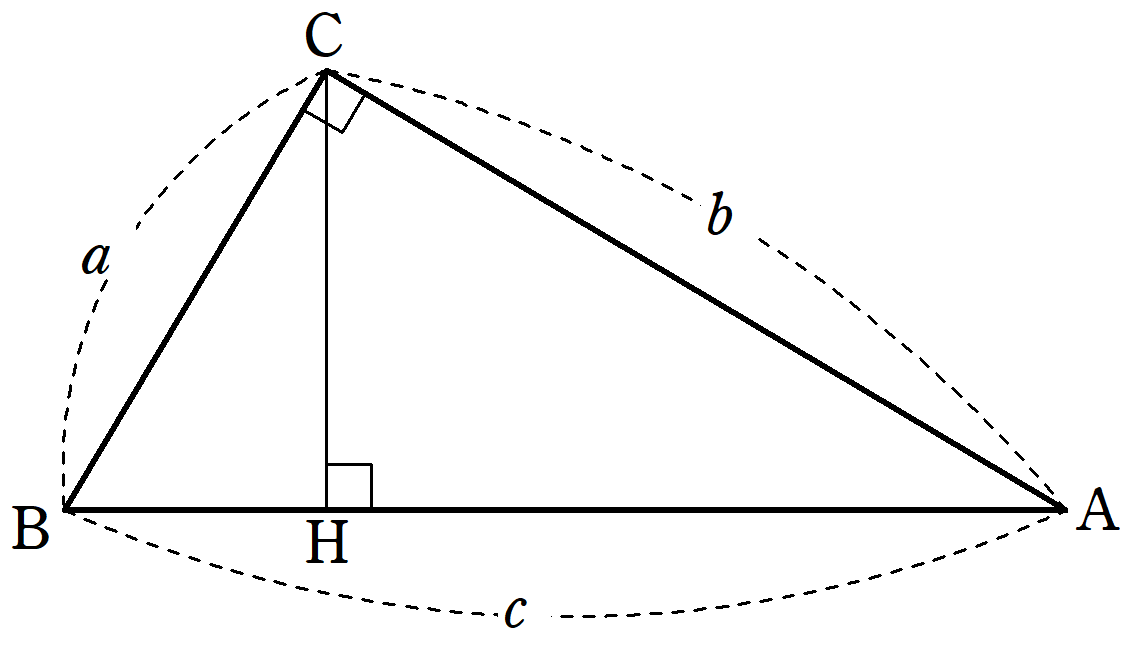
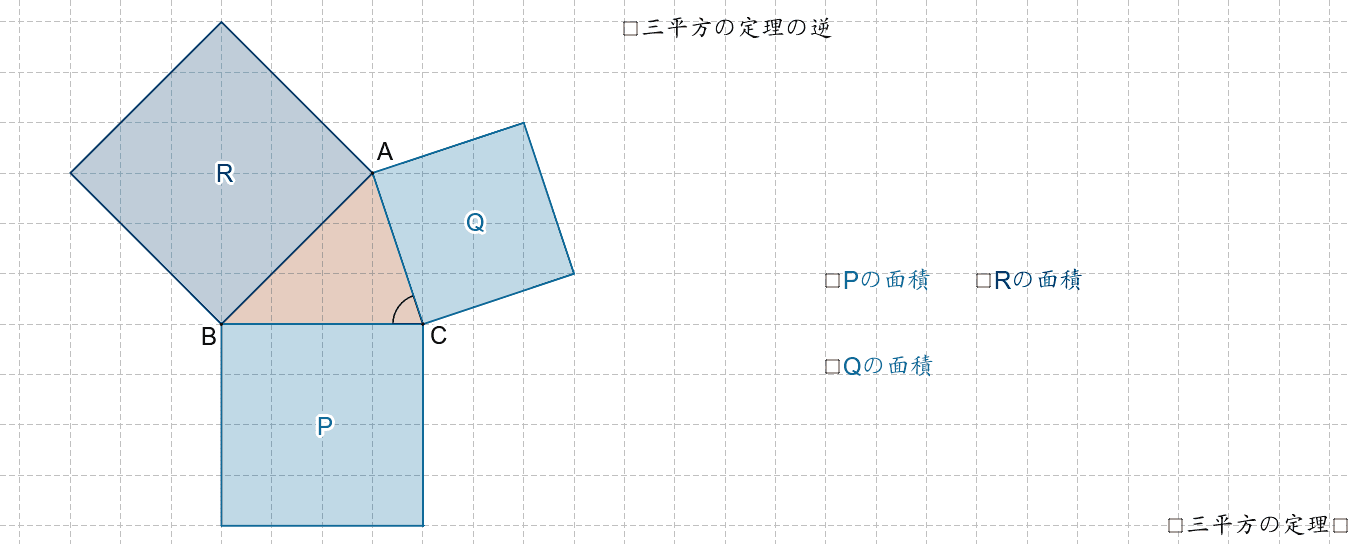
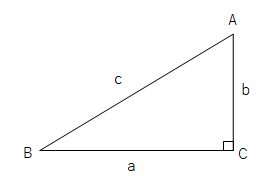
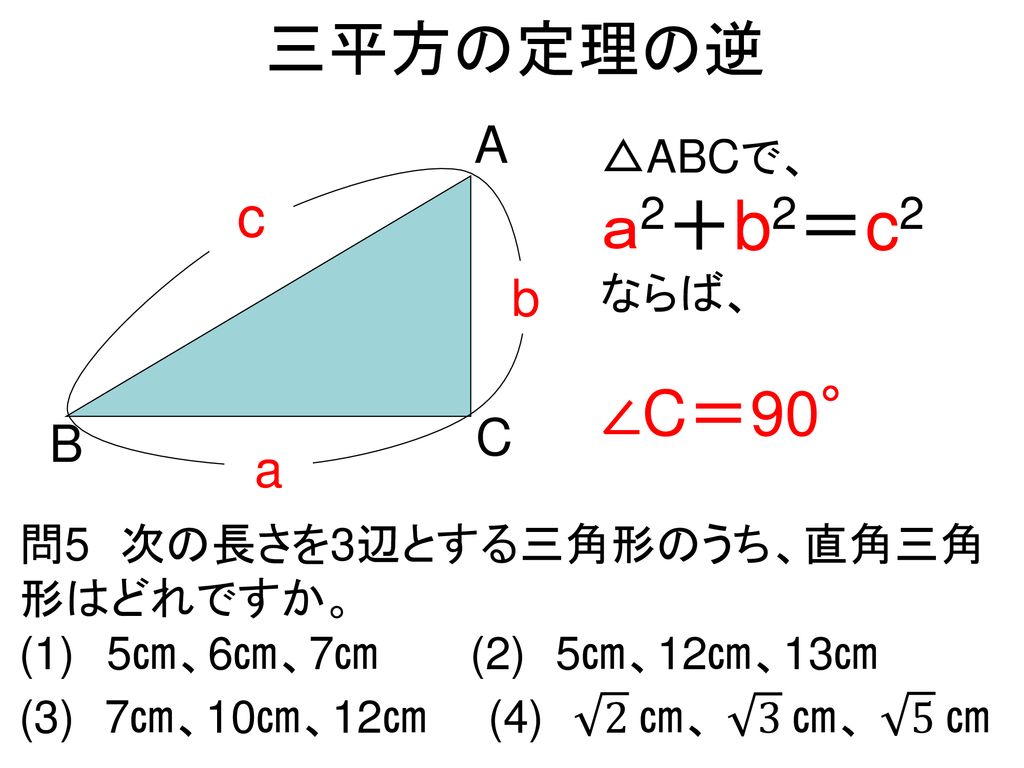
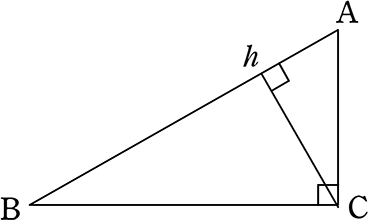
三平方の定理三平方の定理直角三角形の \(3\) 辺の長さには、以下のようの関係式が常に成り立ちます。\(a^2 b^2 = c^2\)※直角三角形の \(3\) 辺で、最も長い辺は直角の向かいの辺で、この辺を斜辺といいます。上の三角形の斜辺は、長さが \(Ccm\) の辺です
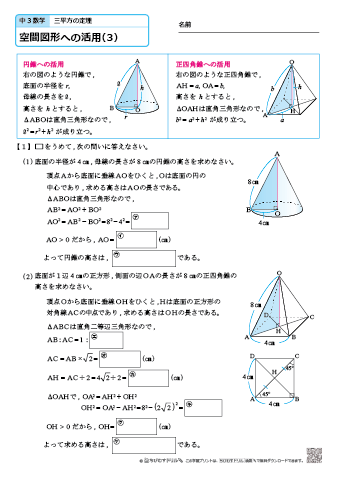
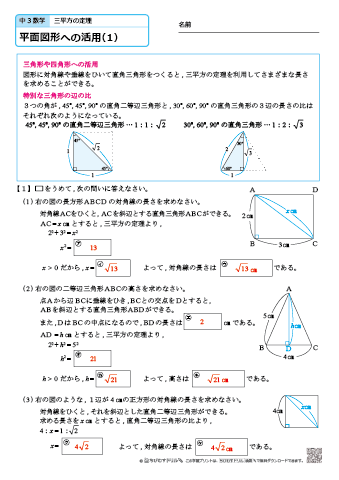
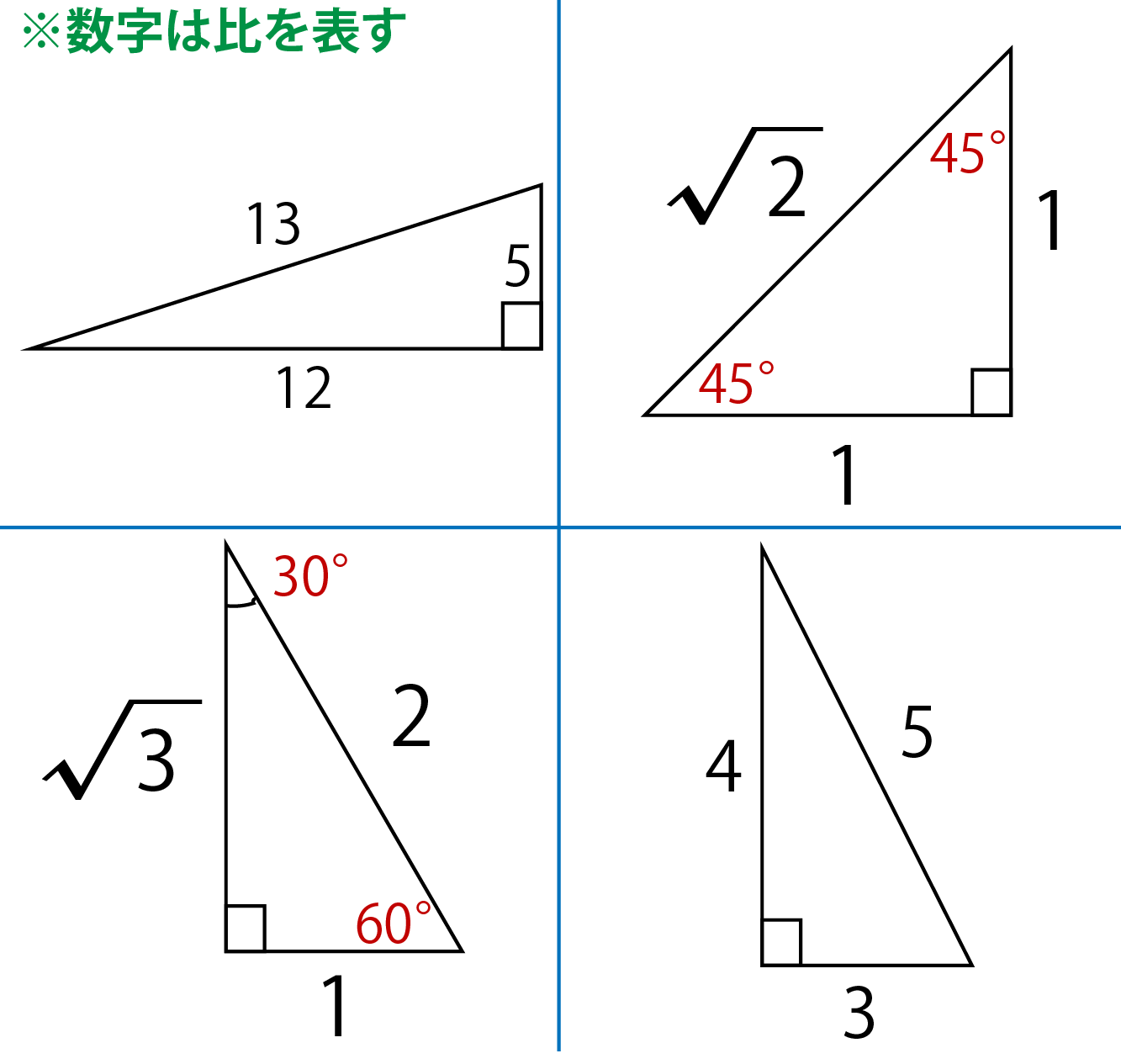
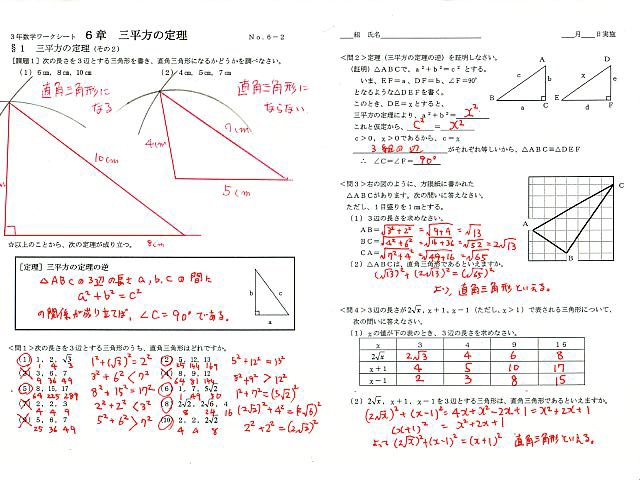
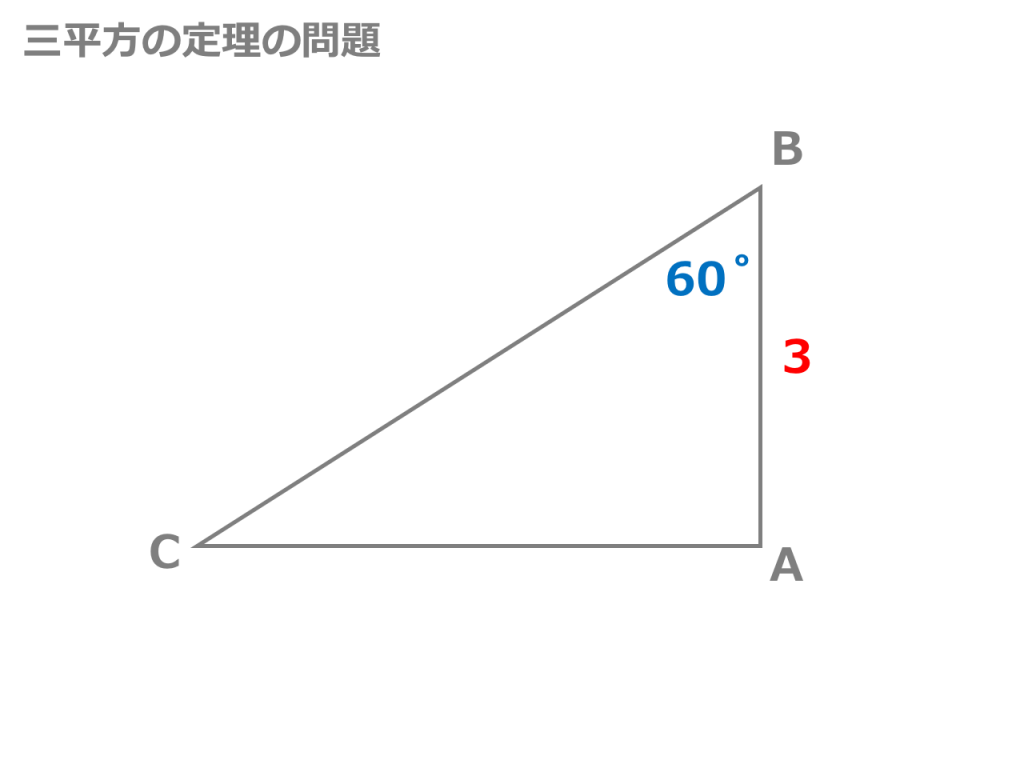
三 平方 の 定理 の 利用-三平方の定理 発展問題まとめ お疲れ様でした! 入試などの発展問題では、今回のように 三平方の定理を使って、方程式を作ることで 長さを求めていくようになります。 まずは、求めたい部分を とする。 直角三角形の各辺を を使って表すことが「平方」とは 2乗のことなので、「三平方の定理」と言われるゆえんは、直角三角形の「三」つの辺それぞれの「平方」、つまり a 2, b 2, c 2 の間に成り立つ関係式ということですね。 代表的な直角三角形の辺の比 三平方の定理を使って、三角定規に使われている 2 つの代表的な直角三角形の辺
三 平方 の 定理 の 利用のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
 |  |  |
「三 平方 の 定理 の 利用」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  | |
 |  | |
「三 平方 の 定理 の 利用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
 |  |  |
「三 平方 の 定理 の 利用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
 |  |  |
「三 平方 の 定理 の 利用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「三 平方 の 定理 の 利用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「三 平方 の 定理 の 利用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「三 平方 の 定理 の 利用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  | |
「三 平方 の 定理 の 利用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |
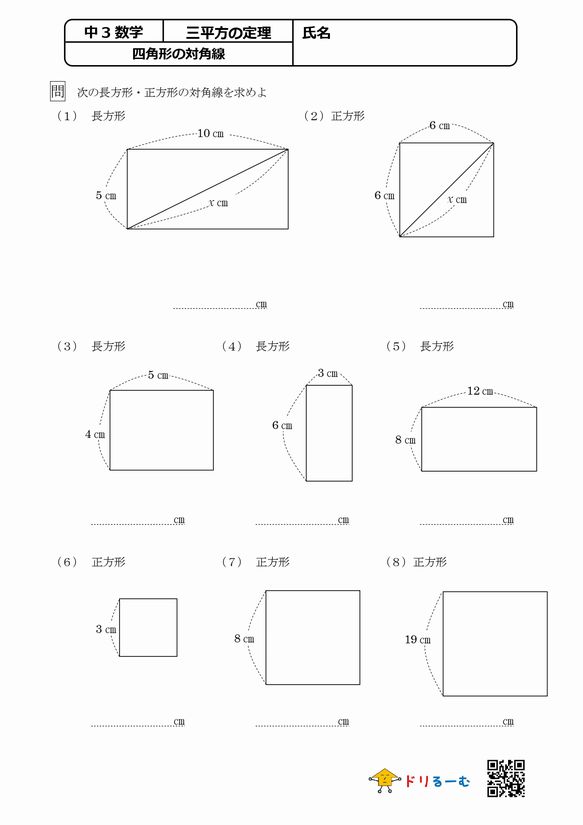
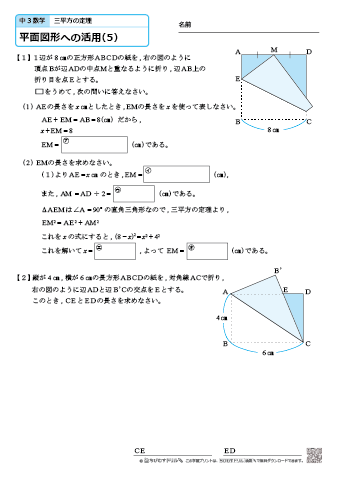
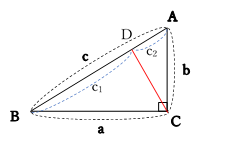
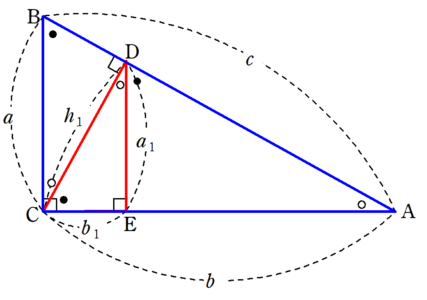
三平方の定理に当てはめて求める問題です。平方根が出てくる場合が多いので、平方根の計算も同時に覚えましょう。 斜辺以外の一辺の長さを求める場合は、三平方の定理を式変形して a² = c² – b² = (cb)(cb) を用いると簡単に解けます。直角三角形 ABE に三平方の定理を適用すると 32AE2=92 AE2=72 AE=6√2nnnn (>0) ABE と BCD は直角三角形で1つの角 B が共通だから「2つの角がそれぞれ等しい」.したがって ABE ∽ BCD 相似三角形の2組の辺の比は等しいから BAAE=BCCD 96√2nnnn=6x 9x=36√2nnnn
コメント
コメントを投稿